Dvojice histogramů a SDCF-výraz

V následujícím obrázku jsou uvedeny histogramy
DHodnoceni / POsob(2) ∧ POsobonoci(vyšší, nejvyšší)
pro podmatice Hotel / HStat(ČR) a Hotel / HStat(Německo) matice dat Hotel.

Pro histogram DHodnocení / POsob(2) ∧ POsobonoci(vyšší, nejvyšší) a matici dat Hotel tedy platí:

• pro podmatici Hotel / HStat(ČR) týkající se 157 hostů z ČR tento histogram roste

• pro podmatici dat Hotel / HStat(Německo) týkající se 72 hostů z Německa tento histogram klesá.

To lze vyjádřit pomocí SDCF-výrazu
HStat(ČR) × HStat(Německo): [↑↓, ≥157, ≥72] DHodnocení / POsob(2) ∧ POsobonoci(vyšší, nejvyšší),
o kterém prohlásíme, že je pravdivý v matici dat Hotel.

Výraz [↑↓, ≥157, ≥72] je SDCF-kvantifikátor. Ověření, zda daný SDCF-výraz je pravdivý v dané matici dat se provádí na základě SDCF-tabulky.

SDCF-výraz má tvar α×β: ≈A/χ kde

• α,β,χ jsou booleovské atributy
• A je kategoriální atribut
• ≈ je SDCF-kvantifikátor.

SDCF-výraz je určen pro vyjádření rozdílu mezi histogramy A/α∧χ a A/β∧χ. Pro popis tohoto rozdílu se používá SDCF-tabulka a SDCF-kvantifikátor.

Histogram A/α∧χ na matici dat M je totéž jako histogram A/χ na podmatici M/α a histogram A/β∧χ na
matici dat M je totéž jako histogram A/χ na podmatici M/β. Rozdíl mezi histogramy A/α∧χ a A/β∧χ na
matici dat M můžeme tedy chápat jako rozdíl mezi histogramem A/χ na podmatici M/α a histogramem
A/χ na podmatici M/β.

SDCF-tabulka udává všechny frekvence potřebné pro ověření pravdivosti SDCF-výrazu α×β:≈A/χ v matici dat M. Značí se SDCF(A,α,β,χ,M). Jedná se o dvojici K-tic celých nezáporných čísel SDCF(A,α,β,χ,M) =
‹ CF_α, CF_β › kde CF_α = ‹ n_α,1,…,n_α,K › a CF_β = ‹ n_β,1,…,n_β,K ›.

Předpokládáme, že atribut A má kategorie a₁,…,a_K. Potom n_α,1,…,n_α,K jsou frekvence kategorií a₁,…,a_K v podmatici dat M/α∧χ a n_β,1,…,n_β,K jsou frekvence kategorií a₁,…,a_K v podmatici dat M/β∧χ.

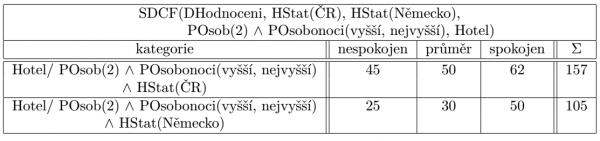
SDCF-tabulku prezentujeme také ve tvaru dle následujícího obrázku

SDCF-tabulka SDCF(Dhodnocení,
HStat(ČR), HStat(Německo), DHodnoceni / POsob(2) ∧ POsobonoci(vyšší, nejvyšší), Hotel)
pro ověření platnosti SDCF-výrazu
HStat(ČR) × HStat(Německo): [↑↓, ≥157, ≥72] DHodnoceni / POsob(2) ∧ POsobonoci(vyšší, nejvyšší),
v matici dat Hotel je v následujícím obrázku.

Symbol ≈ v SDCF-výrazu α×β: ≈A/χ kde se nazývá SDCF-kvantifikátor. Definuje podmínku týkající se dvojice K-tic celých nezáporných čísel C_α a C_β kde C_α = ‹ c_α,1,…,c_α,K › a C_β = ‹ c_β,1,…,c_β,K ›. Podobně jako pro CF-kvantifikátor, chápeme SDCF-kvantifikátor ≈ jako {0,1}-hodnotovou funkci ≈(C_α, C_β) týkající se K-tic C_α a C_β. Platí

• ≈( C_α, C_β) = 1 pokud je podmínka daná SDCF-kvantifikátorem splněna pro K-tice C_α a C_β
• ≈( C_α, C_β) = 0 pokud podmínka daná SDCF-kvantifikátorem pro K-tice C_α a C_β splněna není.

Příkladem SDCF-kvantifikátoru je výraz [↑↓, ≥157, ≥72] použitý ve výše uvedeném příkladu. Tomuto SDCF-kvantifikátoru odpovídá podmínka P:
c_α,1 < c_α,2 <…< c_α,K-1 < c_α,K ∧ c_α,1+…+c_α,K ≥157 ∧
c_β,1 > c_β,2 > … > c_β,K-1 > c_β,K ∧ c_β,1 +…+ c_β,K ≥72.
Tedy:

• [↑↓, ≥157, ≥72](C_α, C_β) = 1 pokud je podmínka P splněna
• [↑↓, ≥157, ≥72](C_α, C_β) = 0 pokud podmínka P splněna není.

SDCF-kvantifikátory implementované v GUHA proceduře SDCF-Miner jsou popsány zde.

Pravdivost SDCF-výrazu α×β: ≈A/χ v matici dat M je definována pomocí SDCF-tabulky
SDCF(A,α,β,χ,M) = ‹ CF_α, CF_β takto:

• α×β: ≈A/χ je pravdivý v matici dat M pokud ≈(CF_α, CF_β) = 1, formálně zapisujeme
  Val(α×β: ≈A/χ, M) = 1
• α×β: ≈A/χ je nepravdivý v matici dat M pokud ≈(CF_α, CF_β) = 0, formálně zapisujeme
  Val(α×β: ≈A/χ, M) = 0.