SD4ft-pravidlo

Příkladem SD4ft-pravidla je výraz
HStat(Slovensko) × HStat(Rakousko): HVek(od 28 do 60) ⇒^*_1.7,31,69 DHodnoceni(nespokojen),
kterému odpovídá výstup procedury SD4ft-Miner uvedený v následujícím obrázku.

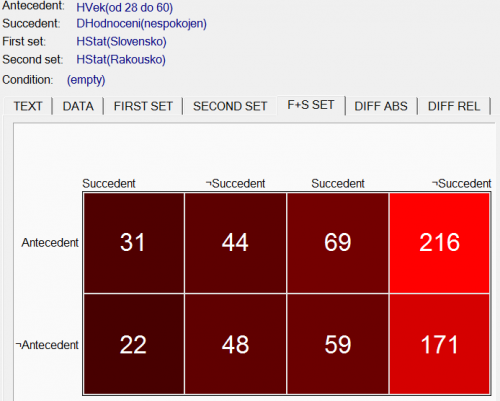
Uvedené SD4ft-pravidlo se týká matice dat Hotel. Platí:

• 4ft(HVek(od 28 do 60), DHodnoceni(nespokojen), Hotel/HStat(Slovensko)) = ‹31,44,22,48›,
  tedy konfidence podmíněného pravidla
  4ft(HVek(od 28 do 60)≈ DHodnoceni(nespokojen) / HStat(Slovensko) = 31/(31+44) = 0.41.
  Jinými slovy, podíl nespokojených hostů ve věku od 28 do 60 je pro Slovensko roven 41 %.

• 4ft(HVek(od 28 do 60), DHodnoceni(nespokojen), Hotel/HStat(Rakousko)) = ‹69,216,59,171›,
  tedy konfidence podmíněného pravidla
  4ft(HVek(od 28 do 60)≈ DHodnoceni(nespokojen) / HStat(Rakousko) = 69/(69+216) = 0.24.
  Jinými slovy, podíl nespokojených hostů ve věku od 28 do 60 je pro Rakousko roven 24 %.

• Podíl nespokojených hostů ve věku od 28 do 60 je pro Slovensko 41/24 = 1.7 krát větší než pro Rakousko a zároveň je 31 nespokojených hostů ze Slovenska a 69 nespokojených hostů z Rakouska ve věku od 28 do 60.

Tento fakt je vyjádřen výše uvedeným SD-pravidlem
HStat(Slovensko) × HStat(Rakousko): HVek(od 28 do 60) ⇒^*_1.7,31,69 DHodnoceni(nespokojen).

SD4ft-pravidlo je výraz α×β:φ∼ψ kde

• α,β,φ,ψ jsou booleovské atributy
• ∼ je SD4ft-kvantifikátor

Booleovský atribut φ se nazývá antecedent, ψ je sukcedent (konsequent), α je definice první množiny a β je definice druhé množiny.

SD4ft-pravidlo α×β:φ∼ψ říká, že vztah booleovských atributů φ a ψ se liší pokud tento vztah posuzujeme jednou na množině řádků dané booleovským atributem α a podruhé na množině řádků daných booleovským atributem β. Odlišnost je dána SD4ft-kvantifikátorem ∼.

Lze také říci, že SD4ft-pravidlo α×β:φ∼ψ vyjadřuje, že podmíněná asociační pravidla φ≈ψ/α a φ≈ψ/β se liší způsobem daným SD4ft-kvantifikátorem ∼.

Určení, zda SD4ft-pravidlo α×β:φ∼ψ je pravdivé v matici dat M se provádí na základě SD4ft-tabulky.

Je možno pracovat i s podmíněnými SD4ft-pravidly.

SD4ft-tabulkou SD4ft(α×β:φ∼ψ, M) pro SD4ft-pravidlo α×β:φ∼ψ a matici dat M se rozumí dvojice ‹T_α, T_β›
4ft-tabulek T_α = 4ft(φ,ψ,M/α) = ‹a_α,b_α,c_α,d_α› a T_β = 4ft(φ,ψ,M/β) = ‹a_β,b_β,c_β,d_β›, viz též následující obrázek.

Symbol „∼“ v SD4ft-pravidle α×β:φ∼ψ se nazývá SD4ft-kvantifikátor. Definuje podmínku týkající se čtveřic celých nezáporných čísel T_α = ‹a_α,b_α,c_α,d_α› a T_β = ‹a_β,b_β,c_β,d_β›. Podobně jako pro 4ft-kvantifikátor, chápeme SD4ft-kvantifikátor ∼ jako {0,1}-hodnotovou funkci ∼(T_α, T_β) týkající se čtveřic celých nezáporných čísel T_α a T_β. Platí

• ∼(T_α, T_β) = 1 pokud je podmínka daná SD4ft-kvantifikátorem splněna pro čtveřice T_α a T_β
• ∼(T_α, T_β) = 0 pokud podmínka daná SD4ft-kvantifikátorem pro čtveřice T_α a T_β splněna není.

Příkladem SD4ft-kvantifikátoru je výraz ⇒^*_1.7,31,69 použitý ve výše uvedeném příkladu. Tomuto SD4ft-kvantifikátoru odpovídá podmínka [a_α/(a_α+b_α)]/[a_β/(a_β+b_β)] ≥ 1.7 ∧ a_α ≥ 31 ∧ a_β ≥ 69. Tedy:

• ⇒^*_1.7,31,69 (T_α, T_β) = 1 pokud platí [a_α/(a_α+b_α)]/[a_β/(a_β+b_β)] ≥ 1.7 ∧ a_α ≥ 31 ∧ a_β ≥ 69
• ⇒^*_1.7,31,69 (T_α, T_β) = 0 pokud neplatí [a_α/(a_α+b_α)]/[a_β/(a_β+b_β)] ≥ 1.7 ∧ a_α ≥ 31 ∧ a_β ≥ 69 .

SD4ft-kvantifikátory implementované v GUHA proceduře SD4ft-Miner jsou popsány zde.

Pravdivost SD4ft-pravidla α×β:φ∼ψ v matici dat M je definována pomocí SD4ft-tabulky
SD4ft(α×β:φ∼ψ, M) = ‹T_α, T_β› takto:

• α×β:φ∼ψ je pravdivé v matici dat M pokud ∼(T_α, T_β) = 1, formálně zapisujeme Val(α×β:φ∼ψ, M = 1
• α×β:φ∼ψ je nepravdivé v matici dat M pokud ∼(T_α, T_β) = 1, formálně zapisujeme Val(α×β:φ∼ψ, M) = 0.

Podmíněné SD4ft-pravidlo je výraz α×β:φ∼ψ/χ. Jedná se o SD4ft-pravidlo vyhodnocované v podmatici dat definované booleovským atributem χ. Platí tedy, že podmíněné SD4ft-pravidlo α×β:φ∼ψ/χ je pravdivé v matici dat M pokud je SD4ft-pravidlo α×β:φ∼ψ pravdivé v matici dat M/χ.

To platí, pokud ∼(T_α, T_β) = 1 kde T_α = 4ft(φ,ψ,M/α∧χ) a T_β = 4ft(φ,ψ,M/β∧χ).