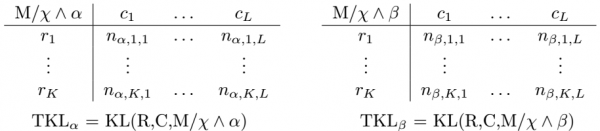SDKL-vztah kategoriálních atributů

SDKL-vztah se týká dvou kategoriálních atributů R a C a dvou podmatic matice dat. Příkladem SDKL-vztahu je vztah kategoriálních atributů DHodnoceni a DPersonal vyjádřený SDKL-výrazem
HMesto(Bratislava) x HMesto(Plzeň): DHodnoceni ≈ PCenaCelkem / PTypPobytu(rekreační),
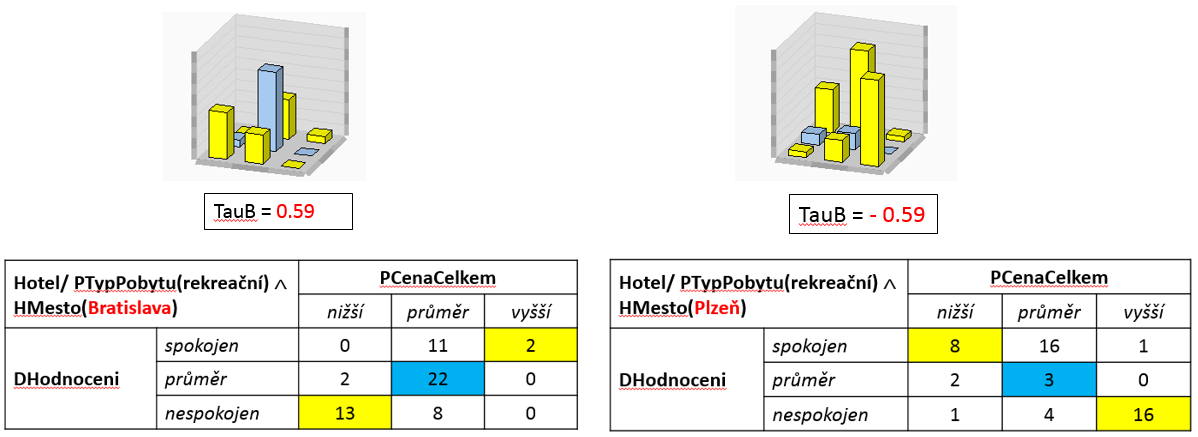
kde symbol ≈ značí SDKL-kvantifikátor [TauB1 ≥ 0.59,TauB2 ≤ -0.59, SUM1 ≥ 58, SUM2 ≥ 51]. Tomuto SDKL-výrazu odpovídá následující obrázek vytvořený z výstupu procedury SDKL-Miner.

Uvedený SDKL-vztah se týká matice dat Hotel. Platí:

• SDKL-vztah se týká atributu DHodnoceni s kategoriemi s kategoriemi nespokojen, průměr, spokojen a atributu PCenaCelkem_ef3 dále označovaného pouze jako PCenaCelkem s kategoriemi nižší, průměr, vyšší.

• SDKL vztah se týká podmatic Hotel / PTypPobytu(rekreační) ∧ HMesto(Bratislava) a Hotel / PTypPobytu(rekreační) ∧ HMesto(Plzeň) říká, že vztah atributů PCenaCelkem a DHodnocení se na těchto podmaticích.

• To lze chápat také tak, že SDKL vztah se týká podmatice Hotel / PTypPobytu(rekreační) a říká, že vztah atributů PCenaCelkem a DHodnocení se na této podmatici liší pokud uvažujeme zvlášť hosty z Bratislavi a zvlášť hosty z Plzně.

• Pokud uvažujeme hosty z Bratislavy, tak je vztah atributů PCenaCelkem a DHodnocení charakterizován Kendallovým koeficientem TauB = 0.59, pro Plzeň to je - 0.59. Z Bratislavy přijelo 58 hostů, z Plzně 51. Podrobnosti viz tabulky a sloupcové grafy v obrázku.

• Lze říci, že pro Bratislavu je mezi atributy pozitivní pořadová korelace, pro Plzeň je to negativní pořadová korelace.

• Výše uvedené je vyjádřeno SDKL-vztahem
  HMesto(Bratislava) x HMesto(Plzeň): DHodnoceni ≈ PCenaCelkem /PTypPobytu(rekreační),
  který platí pro matici dat Hotel a symbol ≈ značí SDKL-kvantifikátor
  [TauB1 ≥ 0.59,TauB2 ≤ -0.59, SUM1 ≥ 58, SUM2 ≥ 51].

SDKL-vztah se týká dvou kategoriálních atributů R a C a dvou podmatic matice dat. Vyjadřuje se SDKL-výrazem α×β: R≈C/χ kde

• α,β,χ jsou booleovské atributy
• R,C jsou kategoriální atributy
• ≈ je SDKL-kvantifikátor

SDKL-vztah α×β: R≈C/χ je určen pro vyjádření rozdílu mezi vztahy kategoriálních atributů R a C na podmaticích daných booleovskými atributy α∧χ a β∧χ. Pro popis tohoto rozdílu se používá SDKL-tabulka a SDKL-kvantifikátor.

Podmatice M/α∧χ matice M je totéž jako podmatice (M/α)/χ matice M/α, analogicky pro M/β∧χ. Rozdíl mezi vztahy kategoriálních atributů R a C na podmaticích M/α∧χ a M/β∧χ matice M je tedy totéž jako rozdíl mezi vztahy atributů R a C za podmínky χ na podmaticích M/α a M/β.

Výrazy SDKL-vztah a SDKL-výraz se obvykle používají jako synonyma.

SDKL-tabulkou SDKL(R,C,α,β,M/χ) pro SDKL-vztah α×β: R≈C/χ a matici dat M rozumíme dvojici KL-tabulek
‹ TKL_α, TKL_β › kde TKL_α = KL(R,C,M/χ∧α) a TKL_β = KL(R,C,M/χ∧β), viz též následující obrázek.

Symbol „≈“ v SDKL-vztahu α×β: R≈C/χ se nazývá SDKL-kvantifikátor. Definuje podmínku týkající se dvojice
‹ {u_α,i,j}, {u_β,i,j} › matic celých nezáporných čísel o K řádcích a L sloupcích. Podobně jako pro 4ft-kvantifikátor, chápeme i SDKL-kvantifikátor ≈ jako {0,1}-hodnotovou funkci ≈({u_α,i,j}, {u_β,i,j}). Platí

• ≈({u_α,i,j}, {u_β,i,j}) = 1 pokud je podmínka daná SDKL-kvantifikátorem ≈ splněna pro matice {u_α,i,j} a {u_β,i,j}

• ≈({u_α,i,j}, {u_β,i,j}) = 0 pokud podmínka daná SDKL-kvantifikátorem ≈ pro matice {u_α,i,j} a {u_β,i,j} splněna není.

SDKL-kvantifikátory implementované v GUHA proceduře SDKL-Miner jsou popsány zde.

Platnost SDKL-vztahu α×β: R≈C/χ v matici dat M je definována pomocí SDKL-tabulky ‹ TKL_α, TKL_β › takto:

• α×β: R≈C/χ platí v matici dat M pokud ≈(TKL_α, TKL_β) = 1, formálně zapisujeme Val(α×β: R≈C/χ, M) = 1

• α×β: R≈C/χ neplatí v matici dat M pokud ≈(TKL_α, TKL_β) = 0, formálně zapisujeme
  Val(α×β: R≈C/χ, M) = 0.