Typové úlohy lze v některých případech chápat jako hledání zajímavých výjimek a odlišností. Dále jsou tyto možnosti stručně naznačeny. Poznamenejme, že úlohy týkající se hledání vhodných podmatic lze chápat jako úlohy subgroup discovery. Podobně, dále uvedené úlohy týkající se asociačních pravidel a výjimek patří do oblasti exception rules mining, viz též informace uvedené zde.

Typové úlohy hledání výjimek a odlišností se týkají

• histogramů, mohou být řešeny procedurou CF-Miner nebo SDCF-Miner
• asociačních pravidel, mohou být řešeny procedurou 4ft-Miner nebo SD4ft-Miner
• kontingenčních tabulek, mohou být řešeny procedurou KL-Miner nebo SDKL-Miner.

Pro histogramy jsou popsány následující typové úlohy na hledání výjimek a odlišností:

1. jiný tvar histogramu na podmatici - CF-Miner
2. jiný tvar histogramu na podmatici podmatice - CF-Miner
3. velká vzdálenost histogramů na podmatici a matici - CF-Miner
4. velká vzdálenost daného histogramu na podmatici podmatice -
   CF-Miner
5. různé tvary histogramu atributu A pro různé kategorie atributu B - SDCF-Miner
6. velká vzdálenost histogramů atributu A pro různé kategorie atributu B - SDCF-Miner
7. výjimky týkající se histogramů pro podíl podmínky na kategoriích - SDCF-Miner.

Úlohy tohoto typu lze charakterizovat takto:

• Vyjdeme z tvaru histogramu na celé matici dat M.
• Určíme tvar histogramu který chápeme jako zajímavou odlišnost k tvaru histogramu na celé matici.
• Vyjádříme tento tvar pomocí CF-kvantifikátoru.
• Definujeme množinu COND relevantních χ jako množinu podmínek pro proceduru CF-Miner.
• Pomocí procedury CF-Miner s případnými korekcemi parametrů najdeme všechny relevantní podmatice M/χ.

Dále jsou uvedeny čtyři příklady ukazující možnosti hledání odlišností k tvaru histogramu na celé matici dat. Všechny příklady jsou již prezentovány jako příklady aplikací procedury CF-Miner. První dva příklady se týkají histogramu atributu PDenTydne matice dat Hotel. Histogram ukazuje procentuální podíl hostů přijíždějících do hotelu v jednotlivých dnech týdne, je uveden na následujícím obrázku.

První příklad se týká situace, kdy za zajímavou odlišnost od celé matice Hotel pokládáme podmatici Hotel/χ na níž jeden sloupec tohoto histogramu významně převyšuje ostatní sloupce. Taková situace je naznačena v levé části následujícího obrázku. Příslušné aplikace procedury CF-Miner jsou popsány zde, zde a zde, obecný postup je zde.

Druhý příklad se týká situace, kdy za zajímavou odlišnost od celé matice Hotel pokládáme pokládáme podmatici Hotel/χ na níž mají všechny sloupce tohoto histogramu přibližně stejnou výšku. Taková situace je naznačena v pravé části následujícího obrázku. Příslušné aplikace procedury CF-Miner jsou popsány zde a zde, obecný postup je zde.

Další dva příklady se týkají histogramu atributu DHodnoceni matice dat Hotel. Histogram ukazuje procentuální podíl jednotlivých kategorií hodnocení, je uveden na následujícím obrázku (součet podílů je 101 díky zaokrouhlovací chybě).

Třetí příklad se týká situace, kdy za zajímavou odlišnost od celé matice Hotel pokládáme podmatici Hotel/χ na níž je tento histogram rostoucí. Taková situace je naznačena v levé části následujícího obrázku. Příslušné aplikace procedury CF-Miner jsou popsány příklady jsou zde a zde, obecný postup je zde. Čtvrtý příklad se týká situace, kdy za zajímavou odlišnost od celé matice Hotel pokládáme pokládáme podmatici Hotel/χ na níž je tento histogram klesající. Taková situace je naznačena v pravé části obrázku. Příslušné aplikace procedury CF-Miner jsou popsány zde, zde a zde.

Úlohy tohoto typu lze charakterizovat takto:

• Vyjdeme z tvaru histogramu na celé matici dat M.
• Najdeme podmatici M/ω na které má daný histogram zajímavý tvar odlišný od jeho tvaru na celé matici dat. Obvykle se použije procedura CF-Miner, je však možné použít například i frekvenční analýzu kategorií.
• Určíme tvar histogramu který chápeme jako zajímavou odlišnost k tvaru histogramu na podmatici M/ω.
• Vyjádříme tento tvar pomocí CF-kvantifikátoru.
• Definujeme množinu COND relevantních ω∧κ jako množinu podmínek pro proceduru CF-Miner.
• Definice COND - relevantních ω∧κ má dvě části. První část je definicí jednoho booleovského atributu ω. Druhá část je definicí množiny relevantních booleovských atributů κ.
• Pomocí procedury CF-Miner s případnými korekcemi parametrů najdeme všechny relevantní podmatice M/ω∧κ.

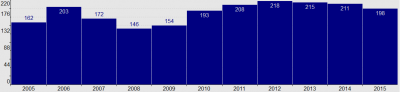
Dále je uveden příklad ukazující možnosti hledání podmatic M/ω∧κ na nichž má histogram jiný tvar než na podmatici M/ω. Jedná se o příklad již prezentovaný jako příklad aplikace procedury CF-Miner. Týká se atributu Year matice dat Accidents. Histogram v levé části následujícího obrázku se týká celé matice Accidents a ukazuje počty dopravních nehod v letech 2005 až 2015. Vidíme, že až na jednu výjimku počty klesají. Obrázek v pravé části ukazuje, že počty nehod na podmatici Accidents/ω týkající se malých motocyklů v městských oblastech rostou. Platí ω = . Zajímá nás tedy, zda existuje podmatice Accidents/ω∧κ na které histogram atributu Year klesá v posledních čtyřech letech (tedy tři roky po sobě). Příklad takového histogramu je na následujícím obrázku. Podrobnosti k příkladu jsou zde.

Úlohy tohoto typu lze charakterizovat takto:

• Vyjdeme z tvaru histogramu na celé matici dat M.
• Určíme minimální vzdálenost histogramu na M/χ od histogramu na M.
• Vyjádříme podmínku na minimální vzdálenost pomocí CF-kvantifikátoru pattern - difference.
• Definujeme množinu COND relevantních χ jako množinu podmínek pro proceduru CF-Miner.
• Pomocí procedury CF-Miner s případnými korekcemi parametrů najdeme všechny relevantní podmatice M/χ.

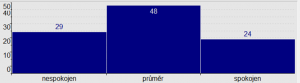
Dále je uveden příklad ukazující možnosti hledání podmatic M/χ takových, že vzdálenost histogramu na M/χ a histogramu na M je velká. Jedná se o příklad již prezentovaný jako příklad aplikace procedury CF-Miner. Týká se histogramu atributu DHodnoceni matice dat Hotel. Histogram ukazuje procentuální podíl jednotlivých kategorií, je uveden v levé části následujícího obrázku (součet podílů je 101 díky zaokrouhlovací chybě). Histogram v pravé části obrázku se týká jisté podmatice M/χ. Vzdálenost těchto histogramů je |29-38| + |48-15| + |24-47| = 65. Příklad uvedený zde se týká situace, kdy hledáme všechny podmatice matice Hotel, pro které platí, že vzdálenost histogramu atributu DHodnocení na podmatici od histogramu tohoto atributu na celé matici dat Hotel je nejméně 50.

Text bude doplněn.

Úlohy tohoto typu lze charakterizovat takto:

• Vyjdeme z atributů A a B takových, že je zajímavé zabývat se odlišnostmi tvaru histogramu atributu A mezi různými kategoriemi atributu B. Příkladem jsou odlišnosti histogramu atributu DHodnoceni mezi různými státy - kategoriemi atributu HStat matice dat Hotel.
• Pomocí vhodných SDCF-kvantifikátorů definujeme dva různé tvary histogramu, jeden pro Operation mode First set frequencies a druhý pro Operation mode Second set frequencies. Například můžeme definovat, že pro First set frequencies histogram roste a že pro Second set frequencies histogram klesá.
• Množiny ALFA a BETA (viz zde a zde) se zadávají jako množina všech základních booleovských atributů B(b), kde b je kategorie atributu B. To znamená, že se použije atribut B s nastavením koeficientů subset 1-1. Je možno použít i jedno nebo dvě nastavení One category. Pokud se toto nastavení použije pro ALFA i BETA, pak musí být obě kategorie různé.
• Pokud nepoužijeme parametr CONDITION, pak porovnáváme histogramy A/B(b₁) a A/B(b₂), kde pouze b₁ a b₂ jsou různé kategorie atributu B. Pokud parametr CONDITION použijeme, pak porovnáváme i histogramy A/χ∧B(b₁) a A/χ∧B(b₂), kde χ je jeden z booleovských atributů zadaných parametrem CONDITION.

Příklad uvedený zde se týká odlišností histogramu atributu DHodnoceni mezi různými státy - kategoriemi atributu HStat matice dat Hotel. Jedná se o příklad již prezentovaný jako příklad aplikace procedury SDCF-Miner. Požadujeme, aby pro jeden stát histogram rostl a pro druhý stát aby klesal, je použit parametr CONDITION. V levé části následujícího obrázku je ukázka histogramu DHodnoceni/χ∧HStat(ČR) který roste, v pravé části je ukázka histogramu DHodnoceni/χ∧HStat(Německo), který klesá.

Text bude doplněn, jedná se o aplikaci procedury SDCF-Miner podobnou předchozí ale s jinými SDCF-kvantifikátory.

Analogické k výše uvedeným možnostem pro histogramy týkající se frekvencí, bude doplněno.

Pro asociační pravidla jsou k dispozici následující typové úlohy na hledání výjimek a odlišností:

1. asociační pravidlo - výjimka z histogramu - 4ft-Miner
2. výrazná změna hodnoty liftu prodloužením antecedentu - 4ft-Miner
3. násobná změna konfidence pravidla dodatečnou podmínkou - SD4ft-Miner
4. různé hodnoty charakteristiky pravidla pro podmatice dané různými kategoriemi atributu - SD4ft-Miner
5. jiné charakteristiky pravidla na podmatici - 4ft-Miner
6. jiné charakteristiky pravidla na podmatici podmatice - 4ft-Miner.

Úlohy tohoto typu lze charakterizovat takto:

• Vyjdeme z histogramu atributu A. Hledáme pravidla φ → A(a_i) taková, že jejich konfidence splňuje jednu z podmínek:
  • je alespoň X-krát nižší, než odpovídá výšce sloupce a_i v histogramu na celé matici dat M
  • je alespoň X-krát nižší, než odpovídá výšce sloupce a_i v histogramu na některé z relevantních podmatic M/✘
  • je alespoň X-krát vyšší, než odpovídá výšce sloupce a_i v histogramu na celé matici dat M
  • je alespoň X-krát vyšší, než odpovídá výšce sloupce a_i v histogramu na některé z relevantních podmatic M/✘
• Požadovanou podmínku nastavíme pomocí vhodného 4ft-kvantifikátoru frequency-difference.
• Jako zadání množiny relevantních antecedentů použijeme zadání relevantních φ.
• Jako zadání množiny relevantních sukcedentů použijeme atribut B s nastavením koeficientů subset 1-1
• Jako zadání množiny relevantních podmínek použijeme zadání množiny relevantních ✘.

Dále jsou uvedeny dva příklady ukazující možnosti hledání asociačních pravidel - výjimek z histogramu. Oba příklady jsou již prezentovány jako příklady aplikací procedury 4ft-Miner. 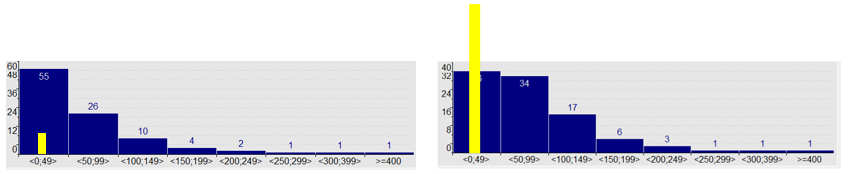První příklad se týká hledání asociačních pravidel φ → A(a_i) takových, že jejich konfidence je alespoň čtyřikrát nižší, než odpovídá výšce sloupce a_i v histogramu na celé matici dat. Taková situace je naznačena v levé části předcházejícího obrázku, podrobnosti jsou k dispozici zde.

Druhý příklad se týká hledání asociačních pravidel φ → A(a_i) takových, že jejich konfidence je alespoň je alespoň dvakrát vyšší, než odpovídá výšce sloupce a_i v histogramu na dané podmatici dat. Taková situace je naznačena v pravé části předcházejícího obrázkupodrobnosti jsou k dispozici zde.

Úlohy tohoto typu lze charakterizovat takto:

• Najdeme zajímavé pravidlo s liftem výrazně vyšším nebo nižším než je jedna. Jeho antecedent chápeme jako podmínku P. To znamená, že relativní četnost sukcedentu za podmínky P je výrazně vyšší nebo nižší než je relativní četnost sukcedentu v celé matici dat.
• Zajímá nás, zda existuje dodatečná podmínka D taková, že pokud platí P i D, pak je relativní četnost téhož sukcedentu výrazně nižší nebo vyšší než je jeho relativní četnost v celé matici dat.

Jako příklad takové úlohy uvádíme úlohu týkající se dat Accidents a problému: Existuje podmínka P, dodatečná podmínka D a závažnost Z nehody takové, že zároveň platí:

• relativní četnost nehod se závažností Z za podmínky P je vyšší než relativní četnost poruch se závažnosti Z mezi všemi nehodami
• relativní četnost nehod se závažností Z je za současné platnosti podmínky P i dodatečné podmínky D nižší, než je relativní četnost nehod se závažnosti Z mezi všemi nehodami?

Ukázka řešení takové úlohy je uvedena zde.

Úlohy tohoto typu lze charakterizovat takto:

• Je dán booleovský atribut ψ pro jehož relativní četnost je za dané podmínky φ příliš nízká nebo příliš vysoká.
• Zajímá nás, za jakých dodatečných podmínek ω se relativní četnost atributu φ násobně zvýší nebo násobně sníží.
• To znamená, že hledáme dvojici asociačních pravidel φ ≈ ψ a φ ∧ ω ≈ ψ takových, že konfidence asociačního pravidla φ ∧ ω ≈ ψ je násobně vyšší nebo nižší, než je konfidence pravidla φ ≈ ψ.

Takové úlohy lze řešit pomocí procedury SD4ft-Miner. Uvedenou úlohu převedeme na úlohu hledání dvojice podmíněných asociačních pravidel True ≈ ψ/φ a True ≈ ψ/φ∧ω takových, že konfidence podmíněného asociačního pravidla True ≈ ψ/φ∧ω je násobně vyšší nebo nižší, než je konfidence podmíněného asociačního pravidla True ≈ ψ/φ. True značí identicky pravdivý booleovský atribut.

Dále jsou uvedeny dva příklady ukazující možnosti hledání dvojic podmíněných asociačních pravidel
True ≈ ψ/φ a True ≈ ψ/φ∧ω takových, že konfidence True ≈ ψ/φ∧ω je násobně vyšší nebo nižší, než je konfidence True ≈ ψ/φ. Oba příklady se týkají dat Hotel a jsou již prezentovány jako příklady aplikací procedury SD4ft-Miner.

První příklad se týká hledání asociačních pravidel True ≈ ψ/φ∧ω takových, že jejich konfidence nejméně 1,5 krát vyšší, než je konfidence podmíněného asociačního pravidla True ≈ ψ/φ. Podrobnosti o příkladu jsou uvedeny zde.

Druhý příklad se týká hledání asociačních pravidel True ≈ ψ/φ∧ω takových, že jejich konfidence je rovna maximálně 0,75 konfidence podmíněného asociačního pravidla True ≈ ψ/φ. Podrobnosti o příkladu jsou uvedeny zde.

Oba příklady lze také chápat jako úlohy na akční pravidla, které ale nejsou řešeny řešena pomocí procedury Ac4ft-Miner.

Úlohy tohoto typu lze charakterizovat takto:

• Je dán atribut A a zajímá nás, zda se zadaným minimálním způsobem liší charakteristiky podmíněných pravidel φ ≈ ψ/A(a₁) a φ ≈ ψ/A(a₂).
• Takovou odlišnost asociačních pravidel potom chápeme jako odlišnost podmatic M/A(a₁) a M/A(a₂) analyzované matice dat M.
• Je možno řešit úlohu nalezení dvojice nejvíce odlišných podmatic M/A(a) a M/A(a') nebo úlohu nalezení podmatice M/A(a), která se nejvíce liší od dané podmatice M/A(a₀).

Takové úlohy lze řešit pomocí procedury SD4ft-Miner. Dále je poukázáno na čtyři úlohy uvedeného typu jejichž řešení je již prezentováno pomocí příkladů aplikací procedury SD4ft-Miner.

První tři úlohy se týkají atributu HStat dat Hotel.

První úloha se týká hledání dvojic států, pro které je pro některé skupiny hostů rozdíl procentuálních podílů nějaké kombinace výsledků v dotazníku větší než daná mez. Pro tuto úlohu jsou k dva příklady. První je popsán v této wiki, je k dispozici i obecný postup pro řešení podobných úloh. Druhý příklad je popsán v pdf-souboru dostupném zde. Ve druhém příkladu je také ukázáno, že tuto úlohu nelze řešit pomocí procedury 4ft-Miner.

Druhá úloha se týká hledání slovanských států, pro které je pro některé skupiny hostů rozdíl procentuálního podíl nějaké kombinace výsledků v dotazníku od téhož podílu v německy mluvících státech větší než daná mez. Pro tuto úlohu je k dispozici příklad popsaný v pdf-souboru dostupném zde.

Třetí úloha se týká hledání dvojic států, pro které je pro některé skupiny hostů podíl procentuálních podílů nějaké kombinace výsledků v dotazníku větší než daná mez. Pro tuto úlohu je k dispozici příklad popsaný v této wiki a také obecný postup pro řešení podobných úloh.

Čtvrtá úloha se týká dat Accidents a řeší otázku rozdílů mezi muži a ženami co se týče relativní četnosti nehod s různou závažností pro různé kombinace charakteristiky řidiče a okolností nehody. Podrobnosti jsou uvedeny zde.

Jedná se o úlohu na podmíněná asociační pravidla. Poznamenejme, že podmíněná asociační pravidla nejsou definována v souvislosti s algoritmem apriori. Tato část bude doplněna. Prozatím je k dispozici obecná úloha na podmíněná pravidla, viz zde.

Jedná se o úlohu na podmíněná asociační pravidla s fixovanou částí podmínky. Tato část bude doplněna.

Pro kontingenční tabulky jsou k dispozici následující typové úlohy na hledání výjimek a odlišností:

Bude doplněno, prozatím lze využít příklady aplikací procedury KL-Miner, viz zde.